 Jo Livingstone
Jo Livingstone
Linear perspective, schmlinear perspective: here are the real shapes that changed how we see.

The Polyhedrists: Art and Geometry in the Long Sixteenth Century,
by Noam Andrews, MIT Press, 316 pages, $44.95
• • •
Since “stadial” history—the idea that societies progress through eras of increasing sophistication over time—went out of fashion, some metanarratives about history’s larger chunks have been discarded, in theory, but never replaced. One of these is the notion that somebody in Italy “invented linear perspective” during the Renaissance and brought forth the modern world.
In this technique, famously developed by the Italian architect Filippo Brunelleschi, objects drawn on paper exist in an imaginary geometric setting plotted along three values; that is, they appear “three-dimensional.” According to the traditional story of the arc of European history, this technological advancement allowed the cultural centers of Europe to throw off the mental shackles of medieval art—whose reverential style constrained artwork to two dimensions—and brought forth a new, modern chain of being. Brunelleschi sits in God’s newly vacant seat, methodically depicting the world in Euclidian space, reconfiguring man’s sense of himself in the universe, and ultimately paving the way for computers and post-painterly abstraction.
The notion that medieval people could not imagine three dimensions or conceive of themselves as individuals is easily extinguished by a quick visit to a medieval cathedral or a skim of any mystical medieval literary confession. Yet historians of culture have thrown everything from Hamlet to the internal combustion engine into the melting pot of a grand Renaissance Humanism that they trace back to Brunelleschi’s conceptual breakthrough of linear perspective. Why?

Jost Amman, Wenzel Jamnitzer, 16th century. Etching, 6 7/8 × 10 3/16 inches. Courtesy Metropolitan Museum of Art.
Part of the reason must be the sheer difficulty of thinking critically about the issue. How can I investigate the way I feel about lines and geometric shapes? On one level, I know that linear perspective is an optical illusion, a kind of spatial metaphor. But our idea of what looks “modern” and “scientific” is so deeply indebted to it that I can’t imagine a world that looks any other way. There’s something about the way linear perspective maps the world onto the page that feels intuitively convincing, or “correct”—conforming to some aspect of reality that’s bigger than the human being. When applied to painting and drawing, a word like “realistic” is predicated on using it properly. Whether or not that reaction is learned or instinctual seems impossible to discern. Linear perspective gives us a feeling of being convinced—of the eye being satisfyingly tricked—that can’t be unwoven from our notion of what the modern world is.
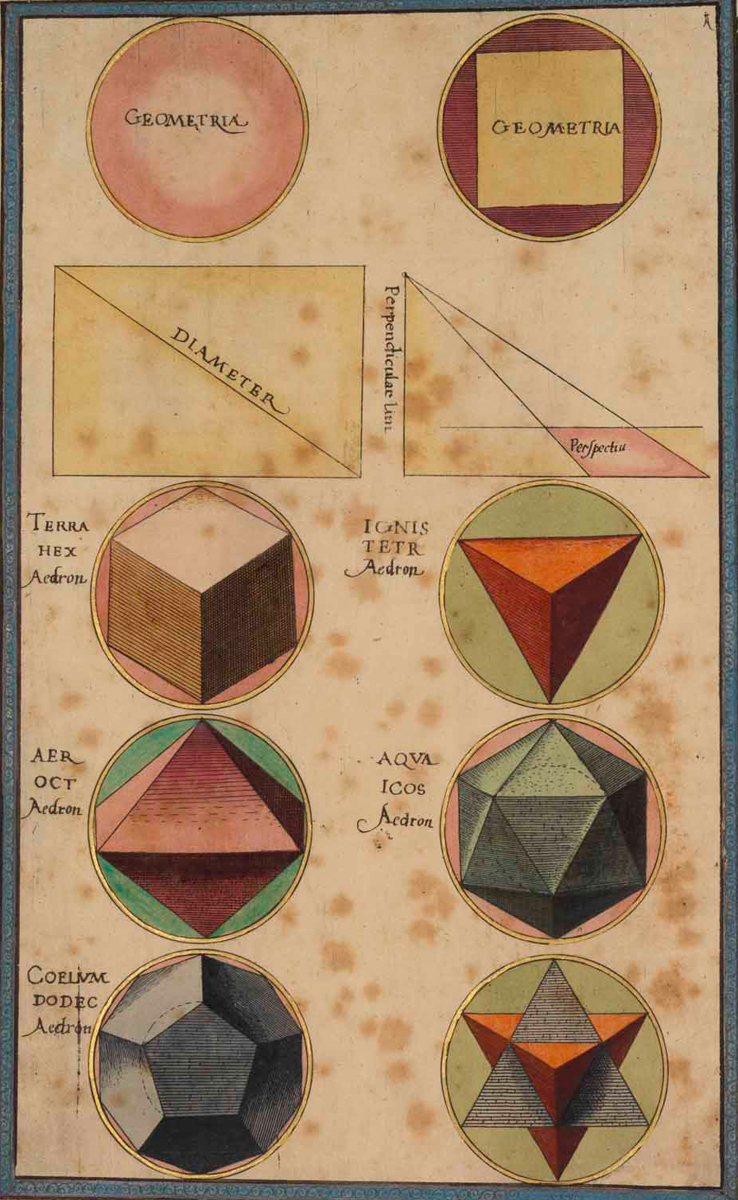
Paul Pfinzing von Henfenfeld, Ein schöner kurtzer Extract der Geometriae vnnd Perspectiuae, 1599. Courtesy Staatsbibliothek Bamberg.
The Polyhedrists: Art and Geometry in the Long Sixteenth Century, a new book by Noam Andrews, takes an ingeniously direct attitude to the problem of the historical third dimension and its relationship to historiography. He gazes directly into Euclidian space, and greets it on its own terms.
Billed as a history of the relationship between art and geometry in the early modern period, the project revolves closely around polyhedra of the sixteenth century and its surrounding years. These “polyhedra” are three-dimensional, convex shapes with flat, polygonal faces and straight edges.

Peter Flötner, Perspectival Drawing of a Column Base with Geometrical Form, 1528. Pen and black ink, brush and bluish gray and brown washes, 4 3/16 × 2 1/2 inches. Courtesy Metropolitan Museum of Art.
They’re just things, really: objects with lots of flat surfaces that look cool and a bit sci-fi and that fascinated the artisans of this period with their otherworldly sleekness. But even when the works at hand are baubles, bits of cabinetry ornamentation, or elephant tusks turned on a lathe to create elaborate objects with polyhedra decorating them, Andrews shows that artists of diverse places and moments in early modern Europe were engaging with three-dimensionality in subtly mathematical ways.
In the geometrical teachings of Euclid, who was the canonical mathematical authority throughout medieval Europe, Andrews writes, scholars had learned all about the five Platonic solids, also termed the regular shapes: the tetrahedron, the cube, the octahedron, the dodecahedron, and the icosahedron. What intrigued a number of influential artisans and artists of early modern Europe, Andrews argues, including famous masters like Albrecht Dürer and Wenzel Jamnitzer and under-acknowledged artisans like Lorentz Stöer, were these regular solids as well as a whole new set of irregular solids—three-dimensional shapes so-called not because they were asymmetrical but because they lay beyond the purview of Euclidian geometry. These were the new, multisided shapes that the polyhedra models articulated.

Augustin Hirschvogel, A True and Thorough Instruction in Geometry (Ein aigentliche und grundtliche anweysung in die Geometria), 1543. Etching. Courtesy Metropolitan Museum of Art.
Such polyhedral shapes, like the rhombicosidodecahedron or the cuboctahedron, are also called the Archimedean solids, because a scholar named Pappus attributed them to a lost chapter of Archimedes’s works. They were technically rediscovered, therefore, rather than identified for the first time. Studying Italian artists like Ugo da Carpi and Parmigianino, and their country’s intellectual exchange with sixteenth-century Germany, Andrews flits over to Nuremberg, where precision engineering became the local export. There, drawings and models of new shapes became both mathematical aides to study and an aesthetic genre of their own—a combination that he explains by pointing to the sumptuous laboratory paintings of Nicolas de Neufchâtel and Jacopo de’ Barbari, which show learned scientists demonstrating knowledge to students using delicate models of polyhedra.
Gradually, and with very close attention to his sources, Andrews argues that these investigations into “irregular” solids, both mathematical and decorative, constitute a signal point in the history of Renaissance mathematics and its relation to the material world. He credits these artists and artisans and scholars with formulating “a new language of abstraction” that was destined for use in engineering and machine-making, even when their works were designed for the inside of a writing desk owned by a rich man.

Paul Pfinzing von Henfenfeld, Ein schöner kurtzer Extract der Geometriae vnnd Perspectiuae, 1599. Courtesy Staatsbibliothek Bamberg.
Linear perspective is part of geometry and math as well as a type of drawing, and mixed mathematical practices like precision engineering have now taken the study of shapes and their surfaces out into every aspect of the world. Andrews helps us to see that this kind of conceptual change was not an ideological transformation at the grandest level of the human mind, but a very specific set of events and works that can be examined closely and without hyperbole.
Fine writing on the actual constituent elements of three-dimensionality is hard to find, pleasing to consume, and pleasurable to recommend. In The Polyhedrists, Andrews dives straight into some bad, old ideas, and returns with multifaceted treasures.
Jo Livingstone is a critic based in New York.